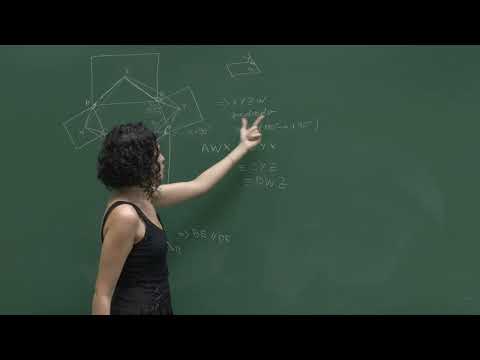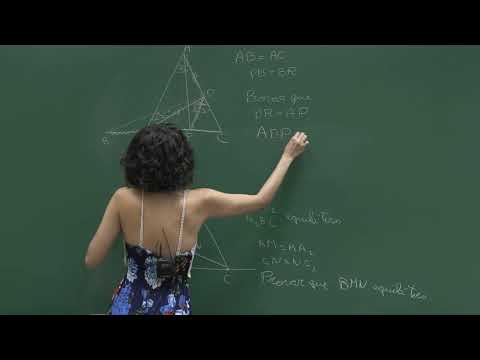Videoaula

Nesta aula apresentamos os casos de congruências de triângulos: LAL, LLL, ALA e LAA. Também observamos que, em geral, ALL não é um caso de congruência, mas é um caso de congruência quando o ângulo é reto.

Utilizando o conceito de congruência de triângulos mostramos que um triângulo tem dois lados iguais se, e somente se, tem dois ângulos iguais. Além disso, mostramos que ao dividir um paralelogramo por uma de suas diagonais obtemos dois triângulos congruentes.

Mostramos que, em um triângulo qualquer, as três mediatrizes se encontram em um único ponto, chamado de circuncentro; e as três alturas se encontram em um único ponto, chamado de ortocentro.

Problema 1. ABCD é um quadrado. Pontos E e F, externos ao quadrado são tais BCE e DCF são triângulos equiláteros. Mostre o triângulo AEF é equilátero. Problema 2. Externamente a um triângulo ABC construímos três triângulos equiláteros AMB, BNC e CPA. Mostre que os segmentos NA, BP e CM são congruentes. Desafio adicional. No Problema 2, mostre que essas três retas se encontram em um mesmo ponto.

Problema 1. Externamente a um paralelogramo ABCD construímos quatro quadrados, com lados comuns aos lados do paralelogramo. Sejam X, Y, Z e W os centros desses quadrados. Mostre que XYZW é um quadrado. Problema 2. ABCD e AECF são paralelogramos. Mostre que BE é paralelo a DF.

Problema 1: começamos com um triângulo isósceles [tex]ABC[/tex] onde [tex]AB=AC[/tex] e o ângulo [tex]A[/tex] mede [tex]36^\circ[/tex]. Traçamos a bissetriz partindo do ponto [tex]B[/tex] até alcançar o ponto [tex]D[/tex]. Formamos assim o triângulo [tex]BDC[/tex] e traçamos a bissetriz partindo do ponto [tex]D[/tex] até alcançar o ponto [tex]P[/tex]. Construímos o ponto [tex]R[/tex] simétrico ao ponto [tex]P[/tex] com relação ao ponto [tex]B[/tex]. Queremos provar que [tex]DR=AP[/tex]. Problema 2: começamos com os pontos [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] colineares e construímos dois pontos [tex]C_1[/tex] e [tex]A_1[/tex] de tal modo que os triângulos [tex]ABC_1[/tex] e [tex]A_1BC[/tex] sejam equiláteros. Construímos os segmentos [tex]CC_1[/tex] e [tex]AA_1[/tex]. Sejam [tex]M[/tex] e [tex]N[/tex] os pontos médios dos segmentos [tex]AA_1[/tex] e [tex]CC_1[/tex] respectivamente. Queremos provar que o triângulo [tex]MNB[/tex] é equilátero.

Problema 1: começamos com um quadrado ABCD. No lado BC pegamos um ponto E e no lado DC pegamos um ponto F de tal modo que EC+CF=AB. Também é dado que o ângulo FAE é igual a 27°. O objetivo é encontrar a soma dos ângulos FBC e EDC. Problema 2: começamos com um triângulo equilátero ABC. Para fora de ABC construímos pontos D, E e F de tal modo que AD=DC=CE=EB=BF=FA. Queremos provar que o triângulo DEF é equilátero.